思考的幻覺: 以問題複雜度透視 LRM 優勢與限制
分類: 軟體 產業新聞 6/9/2025
《思考的幻覺》
副標題: 以「問題複雜度」透視大型推理模型(LRM)的優勢與限制
作者: Parshin Shojaee 、Iman Mirzadeh 、Keivan Alizadeh、Maxwell Horton、Samy Bengio、Mehrdad Farajtabar(Apple)
參考: https://t.ly/UKjV5
摘要與數據速覽
大型推理模型(Large Reasoning Models, LRM)透過 Chain of Thought(CoT)與自我反思機制,在多項推理題上取得突破。然而,當題目複雜度超過某一臨界點,LRM 仍會「思考崩潰」。在作者自建的四款可控謎題中(河內塔、跳棋交換、渡河難題、積木世界),所有前沿 LRM——含 o3 mini、DeepSeek R1 及 Claude 3.7 Sonnet Thinking——都呈現以下共通曲線:
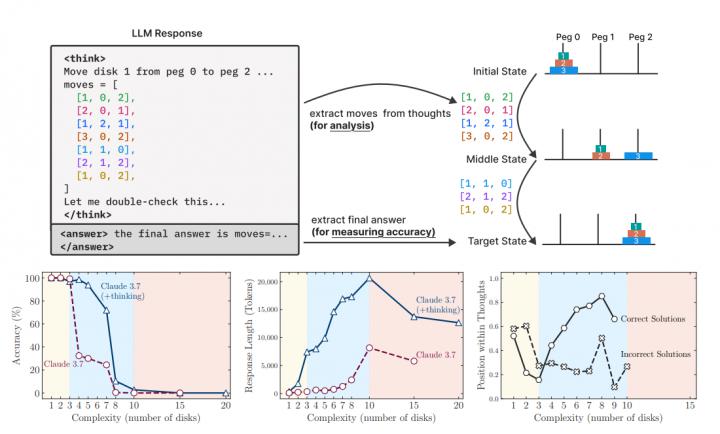
- 正確率三段式:
- 思考 token 反轉:Thinking 版在複雜度升高初期會將思考長度由 ~5 k 逐步拉高到 ~18 k,但一旦接近臨界點,平均思考 token 反而降回 ~10 k,且仍遠低於 64 k 上限。
- 第一個錯步統計:在河內塔 N=10 時,Claude 3.7 Thinking 的首個錯誤通常發生在 第 100 步左右,而同模型於渡河難題 N=3(11 步最佳解)卻常在 第 4 步就踩雷,顯示其「計劃一致性」隨題型劇烈波動。
一、引言
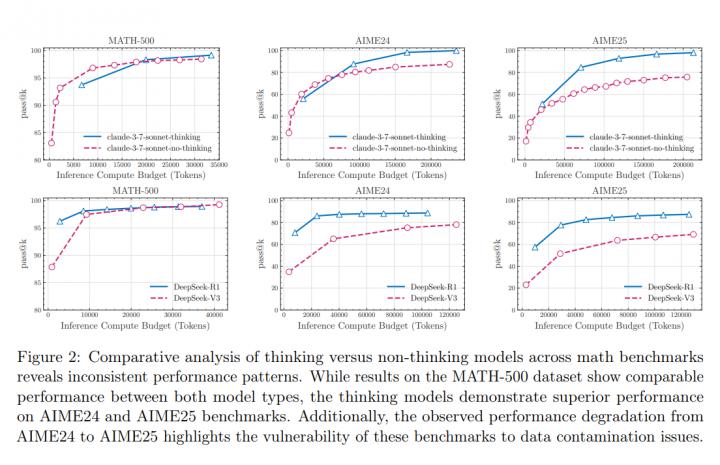
語言模型隨著規模擴張,逐漸加入「明示思考」以強化推理。當前最尖端的 LRM 透過 Chain of Thought 與自我檢查,在 MATH 500、AIME24 等基準上刷新分數,但這些基準易受資料洩漏與難度不均影響。作者因此轉向可逐級調整難度的「小世界」謎題,檢驗 LRM 的真正可擴展性。
---
二、研究設計
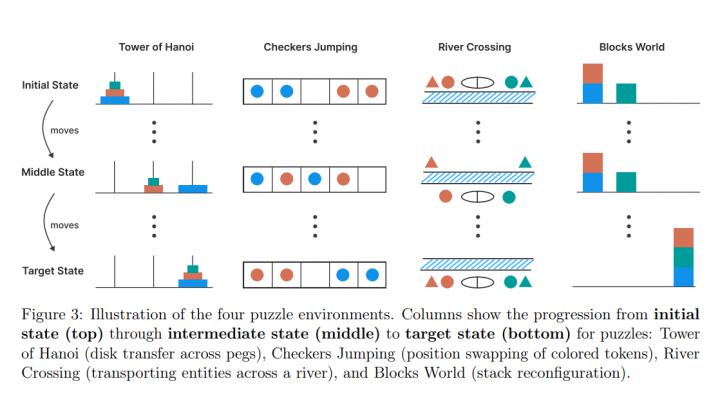
四款謎題皆可用「最短合法步數」作為複雜度刻度:
| 謎題 | 複雜度 N | 最短解長度 | 難度成長 | 最高測試 N |
| 河內塔 | 圓盤數 | 2 1 | 指數 | 20 |
| 跳棋交換 | 每色棋子 n | (n+1)2 1 | 二次 | 10 |
| 渡河難題 | 演員/經紀人對數 | 變量取決於 N、船容 k | 近線性 | 10 |
| 積木世界 | 積木總數 | 取決於初始/目標堆疊 | 近線性 | 60 |
三、實驗結果與分析
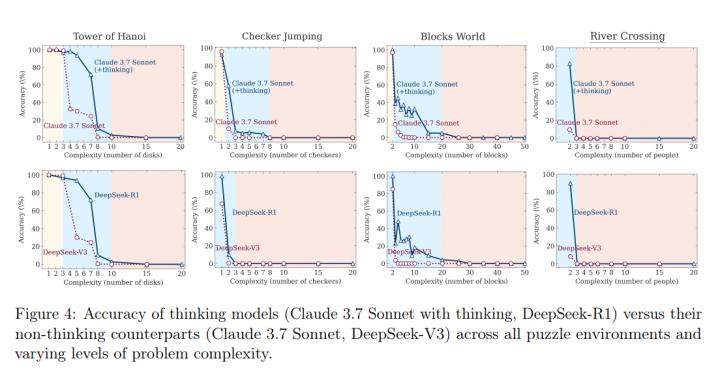
3.1 正確率隨複雜度
圖 4(原論文)展示四謎題的整體正確率曲線。以 Claude 3.7 系列為例:在河內塔,非思考版在 N = 3 仍保持 99 %,Thinking 版約 92 %;
到 N = 7 時,Thinking 版下降到 43 %,非思考版僅 12 %;
而 N 10 兩者皆跌至 0 %,呈崩潰模式。
3.2 思考 token 與崩潰門檻
圖 6 顯示思考 token 與複雜度的雙折線。DeepSeek R1 在河內塔 N = 1 6 間,思考 token 隨 N 從 3 k 緩升到 16 k;一旦 N = 8 以上,token 量急降至 8 10 k,正確率同步趨零。此反直覺現象表明模型在逼近邏輯極限時會「提早放棄推理」。
3.3 中間解路徑:過度思考與延遲修正
透過謎題模擬器,作者截取 Thinking 軌跡中的「候選解」。在簡易題(N = 1 3)中,60 % 的正確解出現在前 30 % 的 tokens,但模型仍繼續生成錯誤路徑,導致最終答案覆蓋率僅 80 %(低於可能的 100 %);在中等題(N = 4 7),正確解往往落在後 50 % 位置,顯示模型需不斷自我修正;複雜題(N 8)則鮮少出現任何正確候選。
3.4 提供演算法也救不了
即便將河內塔完整遞迴演算法附於提示,Claude 3.7 Thinking 的崩潰點仍停留在 N 10,正確率從 31 %(N = 7)斷崖降至 0 %(N = 10)。可見瓶頸不在「找策略」,而在於穩定執行長鏈邏輯。
3.5 第一錯步與失敗分佈
在高複雜度 regime,Thinking 版雖較非思考版更常能撐過前 50 步,但其 首錯步 的離散程度(標準差)是後者的 1.5 2 倍,顯示推理過程波動更大。
四、結論與建議
1. 思考機制價值有限:LRM 僅在「N 4 7」這一中段顯著優於 LLM。當 N 再增,所有模型仍陷入零正確率。 2. 計算資源未被善用:在臨界點附近,模型仍剩餘 >40 k tokens 配額,卻自動縮短思考,暗示 RL 訓練未能學到「持續深想」的策略。 3. 題型敏感度高:同樣 100 步深度,模型可解河內塔卻失手於渡河難題,指出 LRMs 依賴資料分佈而非純粹的算法泛化能力。
對開發者而言,單純延長上下文或堆疊 CoT 長度,難以突破複雜度瓶頸;未來或需在 驗證 修正回圈、符號規劃混合 及 更精細的 RL 獎勵 上尋求突破。
五、研究侷限與後續方向
本研究仍屬「封閉世界」設定,未涵蓋開放式知識檢索或多模態推理。作者建議後續在法律推理、科研假說生成等領域設計可控賽題,並探討「多代理協作」是否能推升臨界複雜度。



